Alex's Blog
0%

发表于 更新于

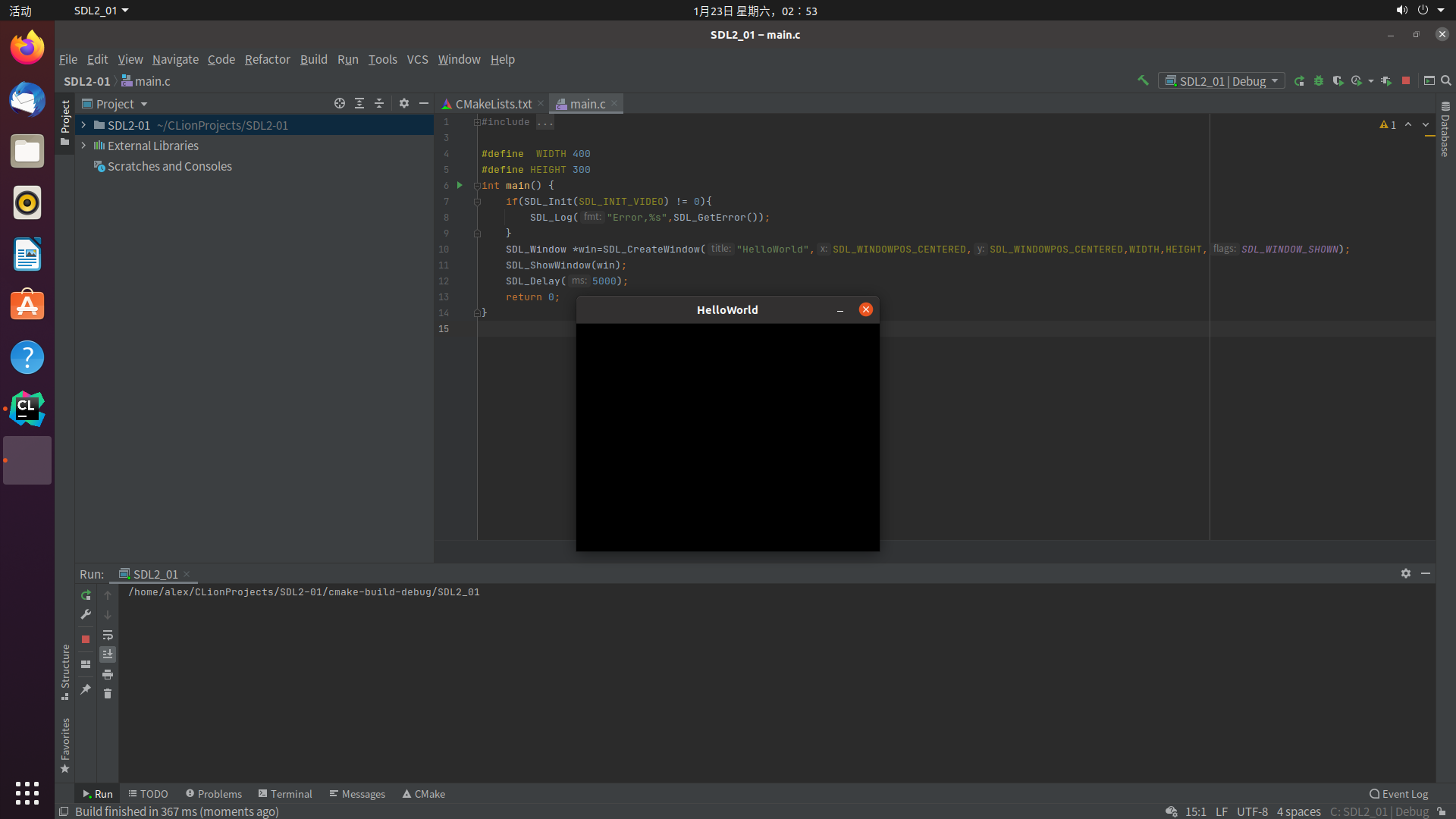
SDL绘制

要在SDL的窗口中绘图 需要先获得 SDL_Surface
SDL提供了SDL_GetWindowSurface(SDL_Window *)来获得客户区的SDL_Surface

1
2
3
4
5
6
SDL_Window *win=SDL_CreateWindow("HelloWorld",
                                SDL_WINDOWPOS_CENTERED,
                                SDL_WINDOWPOS_CENTERED,
                                WIDTH,HEIGHT,
                                SDL_WINDOW_SHOWN);
SDL_Surface *screen=SDL_GetWindowsSurface(win);

获得了SDL_Surface之后 我们有两种方法可以绘制客户区

  • 利用SDL提供的函数


    SDL提供了一些函数来方便绘制
    例如 SDL_FillRect(SDL_Surface *s,SDL_Rect *r,uint32_t color)
    其中 第三个参数是颜色值 按照ARGB顺序排列 每个值为八位
    我们可以利用这个函数将客户区涂成白色
1
2
SDL_Rect r={0,0,WIDTH,HEIGHT};
SDL_FillRect(screen,&r,0xffffffff);

  • 手动绘制


    SDL_Surface是一个结构体,其定义如下
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
typedef struct SDL_Surface
{
    Uint32 flags;               /**< Read-only */
    SDL_PixelFormat *format;    /**< Read-only */
    int w, h;                   /**< Read-only */
    int pitch;                  /**< Read-only */
    void *pixels;               /**< Read-write */

    /** Application data associated with the surface */
    void *userdata;             /**< Read-write */

    /** information needed for surfaces requiring locks */
    int locked;                 /**< Read-only */
    void *lock_data;            /**< Read-only */

    /** clipping information */
    SDL_Rect clip_rect;         /**< Read-only */

    /** info for fast blit mapping to other surfaces */
    struct SDL_BlitMap *map;    /**< Private */

    /** Reference count -- used when freeing surface */
    int refcount;               /**< Read-mostly */
} SDL_Surface;

我们需要关注其中的 w,h 和pixels
w h 分别是宽度和高度
而pixels是一个指向一块内存的指针 此处定义为void *实际使用时可转换为uint32_t *
他对应着屏幕上任意一点处的像素的颜色值 颜色定义为ARGB
而(x,y)处的的像素获取方式为(uint32_t *)pixels[x*w+y]
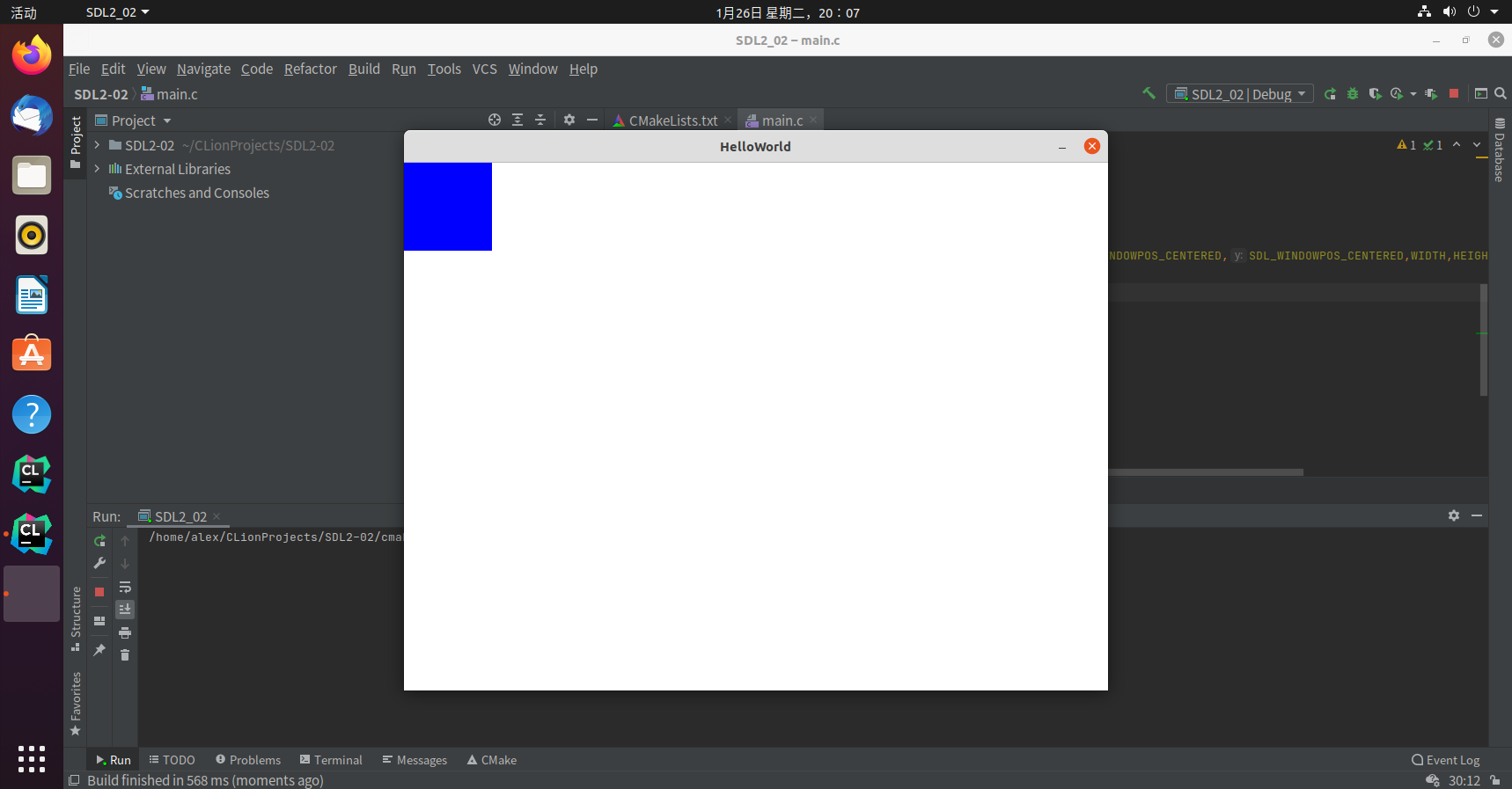
我们通过手动绘制来画一个100x100的方块 放置于(0,0)处

1
2
3
4
5
6
uint32_t *p=(uint32_t *)screen->pixels;
for(int i=0;i<100;i++){
    for(int j=0;j<100;j++){
        p[i*screen->w+j]=0xff0000ff;//ARGB Blue 100%
    }
}

SDL2事件循环

SDL为事件处理提供了灵活的API，当收到来自设备的事件时，SDL会将其存入事件队列等待取出
在程序中，应当有一个循环来处理这些事件，每次循环时应从中取出事件并处理它
SDL 提供了 SDL_PollEvent(SDL_Event *)函数来提供取出事件的功能
如果对列中还有事件 则会取出事件存入SDL_Event类型的变量中 并返回一个非零值 否则返回零
轮询事件后，您可以在逻辑链中响应它。
为了方便阅读 通常会将循环抽出写成一个函数

1
2
3
4
5
6
7
8
9
10
11
12
13
void eventloop(){
    SDL_Event e;
    while(1){
        while(SDL_PollEvent(&e)){
            switch(e.type){
                case SDL_QUIT:
                    return;
                default:
                    break;
            }
        }
    }
}


代码

发表于 更新于

收集自他人提问

回文数是一种很有趣的数，对于一个不是回文数的数，我们可以通过以下操作来将其变成回文数：
将数反转，加到原数上，重复这个过程，直到得到回文数为止

输入格式

输入1个数位不超过1000的正整数

输出格式

对每一个输入，输出将具变成回文数的过程。每一行按以下个数输出：
A + B = C
A是原数，B是反转数，C是和，重复这个过程，直到C是回文数为止。在最后一行输出C is a palindromic number.
为了控制循环次数，我们规定，如果经过10次操作，还得不到回文数，那么停止，显示Not found in 10 iterations.

样例

输入样例1

在这里给出一组输入。例如：

1
1234

输出样例1

在这里给出相应的输出。例如：

1
2
1234 + 4321 = 5555
5555 is a palindromic number

输入样例2

1
1239102349120349

输出样例2

1
2
3
4
5
6
7
8
9
10
11
1239102349120349 + 9430219432019321 = 10669321781139670
10669321781139670 + 07693118712396601 = 18362440493536271
18362440493536271 + 17263539404426381 = 35625979897962652
35625979897962652 + 25626979897952653 = 61252959795915305
61252959795915305 + 50351959795925216 = 111604919591840521
111604919591840521 + 125048195919406111 = 236653115511246632
236653115511246632 + 236642115511356632 = 473295231022603264
473295231022603264 + 462306220132592374 = 935601451155195638
935601451155195638 + 836591551154106539 = 1772193002309302177
1772193002309302177 + 7712039032003912771 = 9484232034313214948
Not found in 10 iterations.

思路

根据输入的格式，不能使用整数来存储输入值，此处采用字符数组存储，将数字直接看作字符串处理，编写对字符串的反转和求和函数，循环十次并判定和是否为回数。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
#include <stdio.h>
#include <string.h>
#define  MAX_COUNT 1050

char num[MAX_COUNT]={0};
char rev[MAX_COUNT]={0};

void reverse(char *src,char *dst,int c){
    for(int i=0,j=c-1;i<c;i++,j--){
        dst[j]=src[i];
    }
}
void add(char *a,char *b,int c){
    int flag=0,num1,num2,sum;
    for(int i=c-1;i>=0;i--){
        num1=a[i]-'0';
        num2=b[i]-'0';
        sum=num1+num2+(flag?1:0);
        if(sum>9){
            sum-=10;
            flag=1;
        }else{
            flag=0;
        }
        a[i]=sum+'0';
    }
    if(flag){
        for(int i=c;i>0;i--){
            num[i]=num[i-1];
        }
        num[0]='1';
    }
}
int isCorrect(char *num,int c){
    int l=0,r=c-1;
    while(l<r){
        if(num[l]!=num[r]) return 0;
        l++;
        r--;
    }
    return 1;
}
int main() {
    scanf("%s",num);
    for(int i=0;i<10;i++){
        reverse(num,rev,strlen(num));
        printf("%s + %s = ",num,rev);
        add(num,rev,strlen(num));
        printf("%s\n",num);
        if(isCorrect(num,strlen(num))){
            printf("%s is a palindromic number.",num);
            return 0;
        }
    }
    printf("Not found in 10 iterations.");
    return 0;
}
BuildPalindromic.c

发表于 更新于

二分查找-1

思路 1：在循环体中查找元素

代码模板

1
2
3
4
5
6
7
8
9
10
11
12
13
int bs(vector<T> &vec,T target){
    int l=0,r=vec.size()-1,mid;
    while(l<=r){
        mid=l+(r-l)/2;
        if(vec[mid]==target)
            return mid;
        else if(vec[mid]<target)
            l=mid+1;
        else 
            r=mid-1;
    }
    return -1;
}

复杂度分析：

  • 时间复杂度 二分查找的时间复杂度是 O(log⁡N) 这里N是输入数组的长度
  • 空间复杂度 由于二分查找算法在执行的过程中只使用到常数个临时变量 因此空间复杂度是 O(1)

细节

  1. 循环可以继续的条件 left<=right 表明区间仅剩一个元素时仍需继续查找
  2. 取中间值 (l+r)/2可能导致l+r发生溢出 所以使用l+(r-l)/2来防止溢出
  3. 取中间值也可以向上取整

练习

374.猜数字大小.cpp 704.二分查找.cpp

发表于 更新于

#
|函数名|函数作用|备注|
|:—-:|:—-:|:—-:|
|SDL_Init|初始化SDL2||
|SDL_CreateWindow|创建窗口||
|SDL_ShowWindow|显示窗口||

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#include <stdio.h>
#include <SDL2/SDL.h>

#define  WIDTH 400
#define HEIGHT 300
int main() {
    if(SDL_Init(SDL_INIT_VIDEO) != 0){
        SDL_Log("Error,%s",SDL_GetError());
    }
    SDL_Window *win=SDL_CreateWindow("HelloWorld",
                                    SDL_WINDOWPOS_CENTERED,
                                    SDL_WINDOWPOS_CENTERED,
                                    WIDTH,HEIGHT,
                                    SDL_WINDOW_SHOWN);
    SDL_ShowWindow(win);
    SDL_Delay(5000);
    return 0;
}

代码

发表于 更新于

使用CMake GUI 完成SDL2的编译（MSVC2019）

Step1.CMake设置

打开CMake(GUI) 设置源码所在文件夹以及存放build文件的文件夹

点击Configure 选择 Visual Studio 16 2019 Finish

等待生成文件

Step2.设置安装目录

修改 CMAKE_INSTALL_PREFIX 的变量值
点击Generate

Step3.开始编译

以管理员身份打开VS2019 打开设置的build存放目录下的SDL2.sln
右击INSTALL 生成 等待编译和复制完成

发表于 更新于

TestPost

1
2
3
4
5
6
7
#include <stdio.h>

int main(){
    printf("HelloWorld");
    return 0;
}

发表于 更新于

实现一个log函数

首先 有换底公式 logab=lnb/lna
由此 求log(b,a)可以转化为求lnb/lna

1
2
3
double mylog(double b,double a){
    return ln(b) / ln(a);
}

接下来只需要编写ln函数
常用的方法是采用多项式展开（泰勒级数）
ln(1+x)展开后为

所以 先将ln(t)中 t 化为 2^k*(1+f) 的形式
其中sqrt(2)/2 < f < sqrt(2)

定义常量

1
2
3
4
#define SQRT2 1.4142135623730950488016887242097
#define SQRT2D2 0.70710678118654752440084436210485
#define LN2H 6.93147180369123816490e-01
#define LN2L 1.90821492927058770002e-10

参数化约

1
2
3
4
5
6
7
8
9
10
11
12
13
14
int k=0;
if(x>SQRT2){
    do
    {
        x/=2;
        k++;
    } while (x>SQRT2);
}else if(x<SQRT2D2){
    do
    {
        x*=2;
        k--;
    } while (x<SQRT2D2);
}

此时 不难看出 ln(t)=ln(2^k*(1+f))=kln2+ln(1+f)
ln(2)在上方已经预先求出并定义

此时只需求出ln(1+f)
为了保证泰勒展开计算的精确度，要使f尽可能接近1，做如下变换
s=f/(2+f)
则ln(1+f)=ln(1+s)-ln(1-s)
此时 做泰勒展开 可得
ln(1+f)=ln(1+s)-ln(1-s)
=2(s-s^3/3+s^5/5+…)
做循环求出该多项式即可

求多项式

1
2
3
4
5
6
7
for(int i=1;i<14;i+=2){
    double s=x;
    for(int c=1;c<i;c++){
        s*=x;
    }
    res+=2*s/i;
}

测试用代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#include <stdio.h>
#include <math.h>
#define SQRT2 1.4142135623730950488016887242097
#define SQRT2D2 0.70710678118654752440084436210485
#define LN2H 6.93147180369123816490e-01
#define LN2L 1.90821492927058770002e-10

double ln(double x){  
    int k=0;
    if(x>SQRT2){
        do
        {
            x/=2;
            k++;
        } while (x>SQRT2);
    }else if(x<SQRT2D2){
        do
        {
            x*=2;
            k--;
        } while (x<SQRT2D2);
    }
    double res=k*LN2H+k*LN2L;
    x-=1;
    x=x/(2+x);
    for(int i=1;i<14;i+=2){
        double s=x;
        for(int c=1;c<i;c++){
            s*=x;
        }
        res+=2*s/i;
    }
    return res;
}

double mylog(double b,double a){
    return ln(b)/ln(a);
}

int main(){
    printf("%lf %lf",mylog(15,2),log(15)/log(2));
    return 0;
}

测试结果

下载源代码文件(log.c)