Alex's Blog
0%

LeetCode-169.多数元素

发表于 更新于

LeetCode-169.多数元素

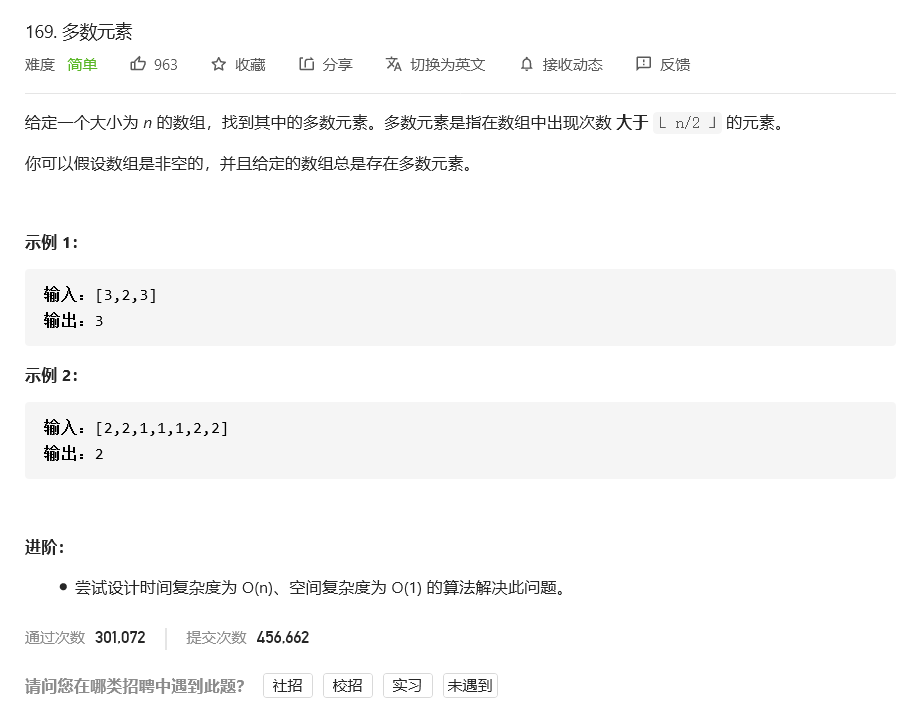
问题描述

思路与解决办法

1. 哈希表

统计每个元素出现的次数 最后取最大的那个即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    int majorityElement(vector<int>& nums) {
        unordered_map<int,int> hashmap;
        for(auto i:nums){
            ++hashmap[i];
        }
        int max=0,max_i=0;
        for(auto it=hashmap.begin();it!=hashmap.end();it++){
            if(it->second>max){
                max=it->second;
                max_i=it->first;
            }
        }
        return max_i;
    }
};


* 时间复杂度:$O(n)$
* 空间复杂度:$O(n)$

{% asset_img 1.png resolution_1 %}

2. 排序

对元素先排序 则$\frac{n}{2}$处的元素一定是众数

1
2
3
4
5
6
7
class Solution {
public:
    int majorityElement(vector<int>& nums) {
        sort(nums.begin(),nums.end());
        return nums.at(nums.size()/2);
    }
};

* 时间复杂度:$O(n\log{n})$
* 空间复杂度:$O(n\log{n})$

{% asset_img 2.png resolution_2 %}

3. 随机化

随机挑选元素 判断是不是众数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int majorityElement(vector<int>& nums) {
        int n=nums.size();
        int halfn=n/2;
        while(1){
            int cand=nums[rand()%n];
            if(count(nums,cand)>halfn) return cand;
        }
    }
    int count(vector<int> &nums,int num){
        int c=0;
        for(auto i:nums){
            c+=i==num?1:0;
        }
        return c;
    }
};


* 时间复杂度:
    理论上最坏情况的时间复杂度是$O(\infty)$ 因为我们可能一直找不到众数
    但是 期望为线性值 
    计算方法如下
    $$
    E\leq{E_{frac{n}{2}}}
    =\lim_{n \to \infty}{\sum_{i=1}^{n}{i*\frac{1}{2^i}}}
    =2
    $$
    每次取随机数后 仍需要$O(n)$时间来判断是不是众数 所以期望的时间复杂度为$O(n)$
* 空间复杂度:$O(1)$

{% asset_img 3.png resolution_3 %}

4. 分治法

易得 若一个数是数组的众数 则他是左半边数组的众数或者是右半边数组的众数
可以使用反证法证明 假设一个数`a`他既不是是左半边数组的众数也不是是右半边数组的众数
根据题目定义 `count(a)`<$\frac{l}{2}+\frac{r}{2}$ 其中`l`和`r`分别是左右两边长度
则`count(a)`<$\frac{l+r}{2}$ 他也不是数组的众数 产生矛盾

我们递归求解 长度为 1 的子数组中唯一的数显然是众数 如果回溯后某区间的长度大于1 我们必须将左右子区间的值合并 如果它们的众数相同 那么显然这一段区间的众数是它们相同的值 
否则 我们需要比较两个众数在整个区间内出现的次数来决定该区间的众数


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
    int count(vector<int> &nums,int target,int lo,int hi){
        int c=0;
        for(int i=lo;i<=hi;i++){
            if(nums[i]==target) c++;
        }
        return c;
    }
    int work(vector<int> &nums,int lo,int hi){
        if(lo==hi) return nums[lo];
        int mid=lo+(hi-lo)/2;
        int left=work(nums,lo,mid);
        int right=work(nums,mid+1,hi);
        if(count(nums,left,lo,hi)>(hi-lo+1)/2)
            return left;
        if(count(nums,right,lo,hi)>(hi-lo+1)/2)
            return right;
        return -1;
    }
public:
    int majorityElement(vector<int>& nums) {
        return work(nums,0,nums.size()-1);
    }
};

* 时间复杂度:
    函数将求解2个长度为$\frac{n}{2}$的子问题 并作两遍扫描 即
    $$
        O(n)=2*T(\frac{n}{2})+2n
    $$
    根据[主定理](https://baike.baidu.com/item/%E4%B8%BB%E5%AE%9A%E7%90%86/3463232?fr=aladdin)
    $$
        T(n)=\Theta(n\log_{b}{a}\log{n})=\Theta(n\log_{2}{2}\log{n})=\Theta(n\log{n})
    $$ 
    即为$O(n\log{n})$

* 空间复杂度:$O(\log{n})$ 来自于递归的栈消耗 数组长度变为1前递归$\log{n}$次

{% asset_img 4.png resolution_4 %}

5. Boyer-Moore 投票算法

维护一个候选数字 `cand` 和他出现的次数 `count` `cand`初始化为任意值 `count`初始化为0
遍历数组 对于每个元素`x`
- 若`count==0` 则`cand=x`
- 继续判断`x`
    - 若`x==cand` 则`count+=1`
    - 否则 `count-=1`
遍历完成后 `cand` 的值就是众数


1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public:
    int majorityElement(vector<int>& nums) {
        int cand=0,count=0;
        for(auto x:nums){
            if(count==0) cand=x;
            if(x==cand) count++;
            else count--;
        }
        return cand;
    }
};

* 时间复杂度: $O(n)$
* 空间复杂度: $O(1)$

{% asset_img 5.png resolution_5 %}