Alex's Blog
0%

LeetCode.354.俄罗斯套娃信封问题

发表于 更新于

LeetCode.354.俄罗斯套娃信封问题

问题描述

解题思路及代码

题目的本质是找出一个最长的二维数组序列 满足其在两个维度上都严格递增(不包含相等的情况)

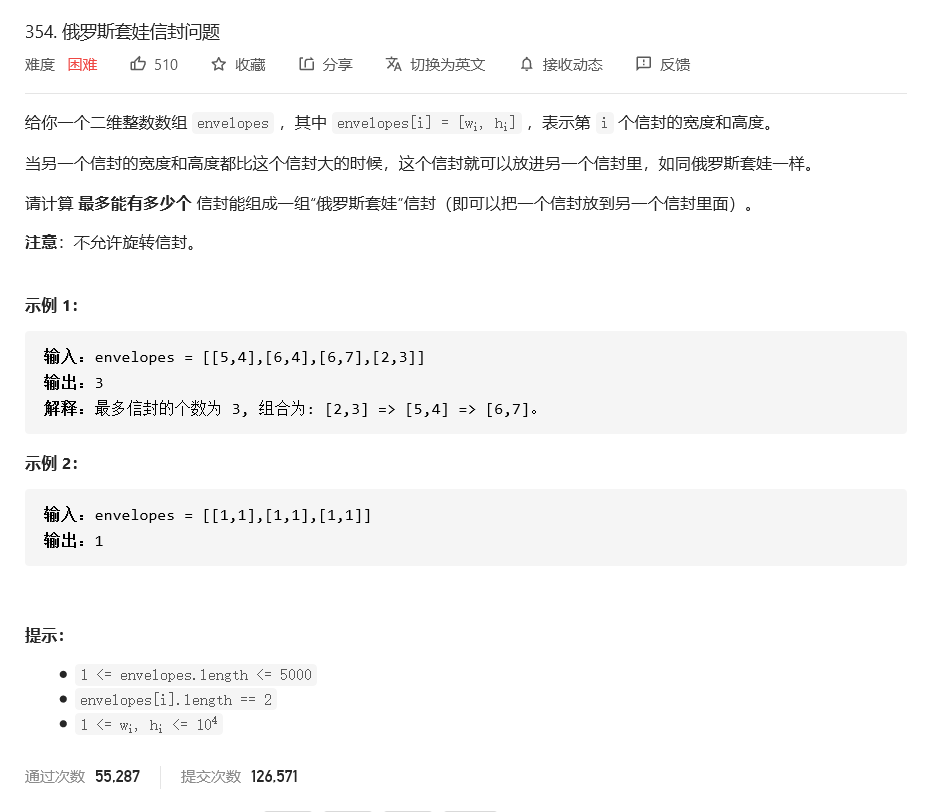
思路一

两个维度都使用 排序法 使两个维度都递增 然后使用动态规划

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int maxEnvelopes(vector<vector<int>>& envelopes) {
        int n=envelopes.size();
        if(!n) return 0;
        sort(envelopes.begin(),envelopes.end()); //两个维度升序排序
        vector<int> dp(n,1); //动态规划记忆化数组
        for(int i=0;i<n;i++){
            for(int j=0;j<n;j++){
                if(envelopes[i][0]>envelopes[j][0]&&
                   envelopes[i][1]>envelopes[j][1]){ //找到符合条件的信封
                    dp[i]=max(dp[i],dp[j]+1); //取较大值
                }
            }
        }
        return *max_element(dp.begin(),dp.end()); //直接返回最大值
    }
};
  • 时间复杂度 $O(n^2)$
  • 空间复杂度 $O(n)$
  • 该解法在部分语言下会超时

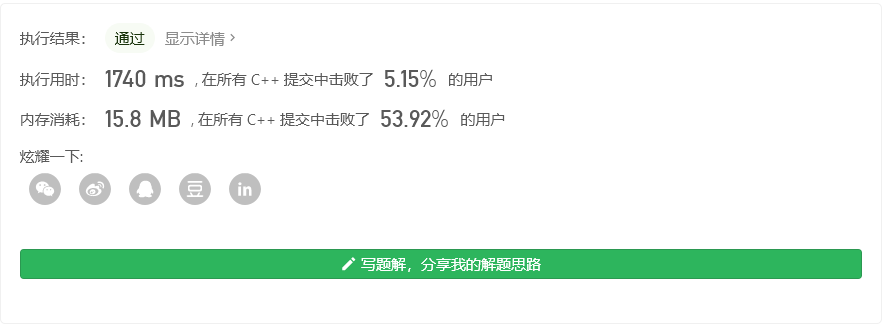
思路二

第一个维度升序 第二个维度降序 最后动态规划

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    int maxEnvelopes(vector<vector<int>>& envelopes) {
        int n=envelopes.size();
        if(!n) return 0;
        sort(envelopes.begin(),envelopes.end(),[](auto &a1,auto &a2){
            return a1[0]<a2[0]||(a1[0]==a2[0]&&a1[1]>a2[1]);
        });
        /*
            使用C++的匿名函数[](){} 传递sort的第三个参数 该参数用于判断是否需要交换两个值
        */
        vector<int> dp(n,1);
        for(int i=0;i<n;i++){
            for(int j=0;j<i;j++){
                if(envelopes[j][1]<envelopes[i][1]){ //动态规划第二维度 
                    dp[i]=max(dp[i],dp[j]+1);
                }
            }
        }
        return *max_element(dp.begin(),dp.end());
    }
};
  • 时间复杂度 $O(n^2)$ 其中n是数组envelopes的长度 排序的时间复杂度为$O(n\log{n})$ 动态规划的时间复杂度为$O(n^2)$
  • 空间复杂度 $O(n)$

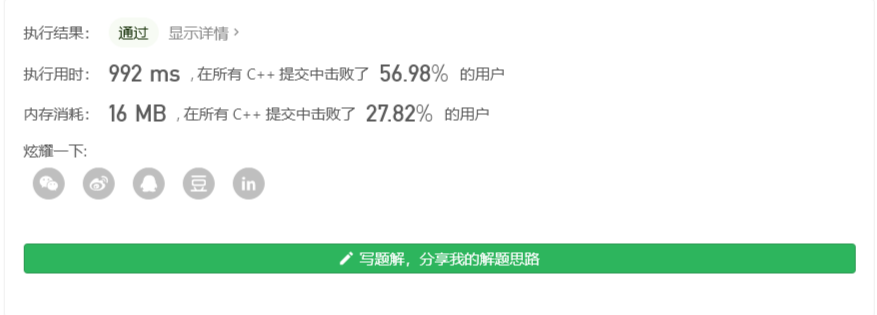
思路三

在思路二的基础上 排序后维护一个数组$f$ 对envelopes二分搜索
考虑当前元素$h_i$

  • 若$h_i$大于f中最大值 则$h_i$可以连接在之后成为一个更长的严格递增序列
  • 否则我们找出 $f$ 中比 $h_i$​ 严格小的最大的元素 $f[j_0]$ 即 $f[j_0]<h_i<=f[j_0+1]$ 那么 $h_i$​ 可以接在$f[j_0]$之后，形成一个长度为$j_0+1$的严格递增子序列，因此需要对$f[j_0+1]$进行更新

最后$f$的长度即所求

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    int maxEnvelopes(vector<vector<int>>& envelopes) {
        int n=envelopes.size();
        sort(envelopes.begin(),envelopes.end(),[](auto a1,auto a2){
            return a1[0]<a2[0]||(a1[0]==a2[0]&&a1[1]>a2[1]);
        });
        vector<int> f;
        f.emplace_back(envelopes[0][1]);
        for(int i=1;i<n;i++){
            int num=envelopes[i][1];
            if(num>f.back()){
                f.emplace_back(num);
            }
            else{
                auto it=lower_bound(f.begin(),f.end(),num);
                *it=num;
            }
        }
        return f.size();
    }
};
  • 时间复杂度 $O(n\log{n})$ 其中n是数组envelopes的长度 排序的时间复杂度为$O(n\log{n})$ 动态规划的时间复杂度为$O(n\log{n})$
  • 空间复杂度 $O(n)$