Alex's Blog
0%

LeetCode87.扰乱字符串

发表于 更新于

LeetCode87.扰乱字符串

部分转载自以下链接:
LeetCode-Solution
jerry_nju

题目描述

使用下面描述的算法可以扰乱字符串 s 得到字符串 t :

  1. 如果字符串的长度为 1 ,算法停止
  2. 如果字符串的长度 > 1 ,执行下述步骤：
    1. 在一个随机下标处将字符串分割成两个非空的子字符串。即，如果已知字符串 s ，则可以将其分成两个子字符串 x 和 y ，且满足 s = x + y 。
    2. 随机 决定是要「交换两个子字符串」还是要「保持这两个子字符串的顺序不变」。即，在执行这一步骤之后，s 可能是 s = x + y 或者 s = y + x 。
    3. 在 x 和 y 这两个子字符串上继续从步骤 1 开始递归执行此算法.

给你两个 长度相等 的字符串 s1 和 s2，判断 s2 是否是 s1 的扰乱字符串。如果是，返回 true ；否则，返回 false .

示例

示例一

1
2
3
4
5
6
7
8
9
10
11
输入：s1 = "great", s2 = "rgeat"
输出：true
解释：s1 上可能发生的一种情形是：
"great" --> "gr/eat" // 在一个随机下标处分割得到两个子字符串
"gr/eat" --> "gr/eat" // 随机决定：「保持这两个子字符串的顺序不变」
"gr/eat" --> "g/r / e/at" // 在子字符串上递归执行此算法。两个子字符串分别在随机下标处进行一轮分割
"g/r / e/at" --> "r/g / e/at" // 随机决定：第一组「交换两个子字符串」，第二组「保持这两个子字符串的顺序不变」
"r/g / e/at" --> "r/g / e/ a/t" // 继续递归执行此算法，将 "at" 分割得到 "a/t"
"r/g / e/ a/t" --> "r/g / e/ a/t" // 随机决定：「保持这两个子字符串的顺序不变」
算法终止，结果字符串和 s2 相同，都是 "rgeat"
这是一种能够扰乱 s1 得到 s2 的情形，可以认为 s2 是 s1 的扰乱字符串，返回 true

示例二
1
2
输入：s1 = "abcde", s2 = "caebd"
输出：false

示例三
1
2
输入：s1 = "a", s2 = "a"
输出：true

思路与方法

显然 若s和t长度不同 则必不能由s变化为t
若长度相同 则存在一个分割点i1,使s分割为s1和s2,一个分割点i2,使t分割为t1和t2

满足

  • 没交换 s1->t1 s2->t2
  • 交换了 s2->t1 s1->t2

子问题

分别讨论两种情况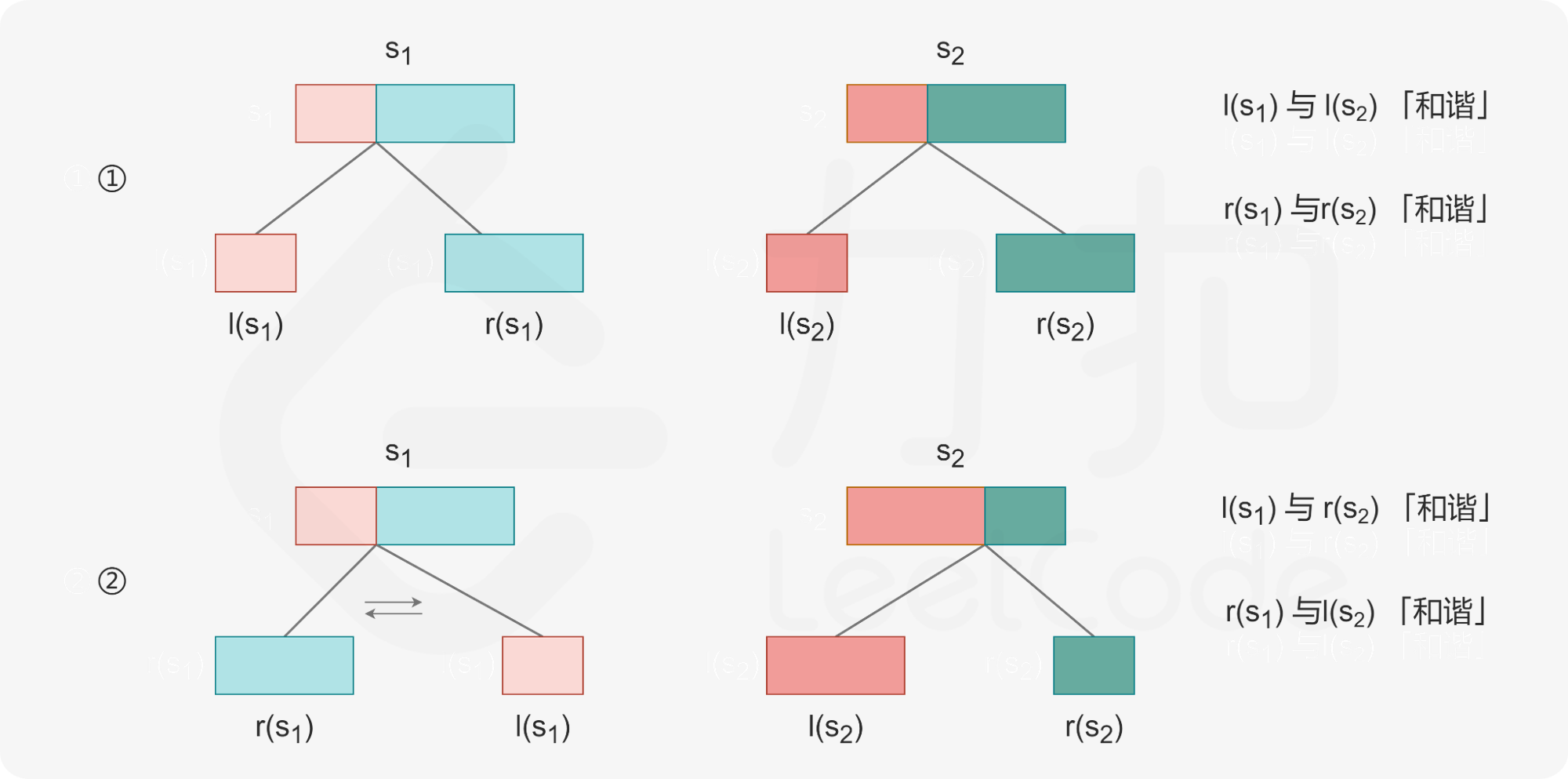

记忆化搜索数组
可先设记忆化搜索数组为mem[i][j][k][h]
又因为s和t长度的关系 j-i=h-k
则可将数组降低为三维 mem[i][j][l]
表示从字符串 s 中 i 开始长度为 l 的字符串是否能变换为从字符串 t 中 j 开始长度为 l 的字符串

状态转移方程

初始条件
对于长度为1的串 只有相等才能变换得到 相等为 true 不相等为 false

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
class Solution {
public:
    int mem[30][30][31];
    string s1,s2;
    bool check(int i1,int i2,int l){
        unordered_map<char,int> freq;
        for(int i=i1;i<i1+l;i++){
            freq[s1[i]]+=1;
        }
        for(int i=i2;i<i2+l;i++){
            freq[s2[i]]-=1;
        }
        for(auto it=freq.begin();it!=freq.end();it++){
            if(it->second!=0)return false;
        }
        return true;
    }
    bool dfs(int i1,int i2,int l){
        if(mem[i1][i2][l])
            return mem[i1][i2][l]==1;
        if(s1.substr(i1,l)==s2.substr(i2,l)){
            mem[i1][i2][l]=1;
            return true;
        }
        if(!check(i1,i2,l)){
            mem[i1][i2][l]=-1;
            return false;
        }
        for(int i=1;i<l;i++){
            if(dfs(i1,i2,i)&&dfs(i1+i,i2+i,l-i)){
                mem[i1][i2][l]=1;
                return true;
            }
            if(dfs(i1,i2+l-i,i)&&dfs(i1+i,i2,l-i)){
                mem[i1][i2][l]=1;
                return true;
            }
        }
        mem[i1][i2][l]=-1;
        return false;
    }
    bool isScramble(string s1, string s2) {
        memset(mem,0,sizeof(mem));
        this->s1=s1;
        this->s2=s2;
        return dfs(0,0,s1.size());
    }
};