AHP

层次分析法 AHP

针对问题类型

适用于解决评价类问题
可以使用打分法解决评价类问题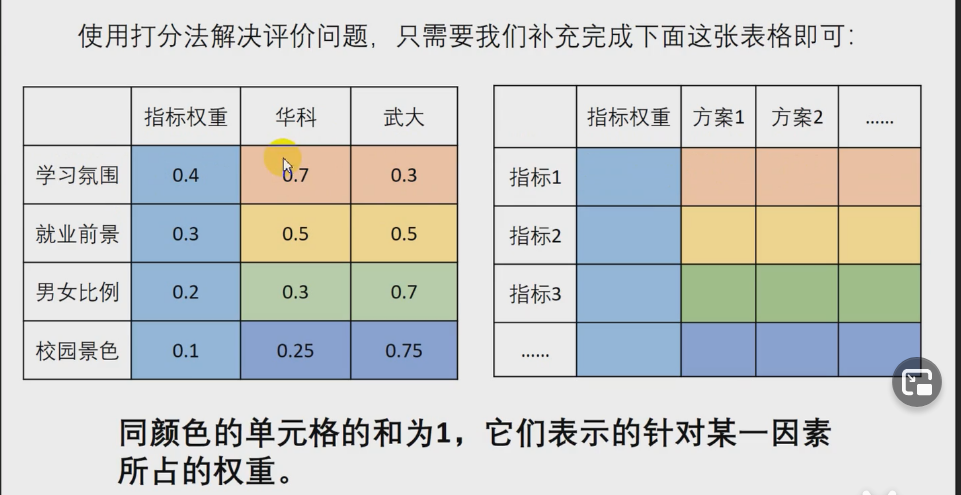

如何解决评价类问题

明确三个问题

1. 我们评价的目标
2. 为了达到这个目标有几种方案
3. 评价的准则、指标

---

搜索文献地址

知网
Google学术
百度学术

如何确定指标权重及各项的分数

分而治之:
一次性考虑这五个指标之间的关系,往往考虑不周
解决方法:
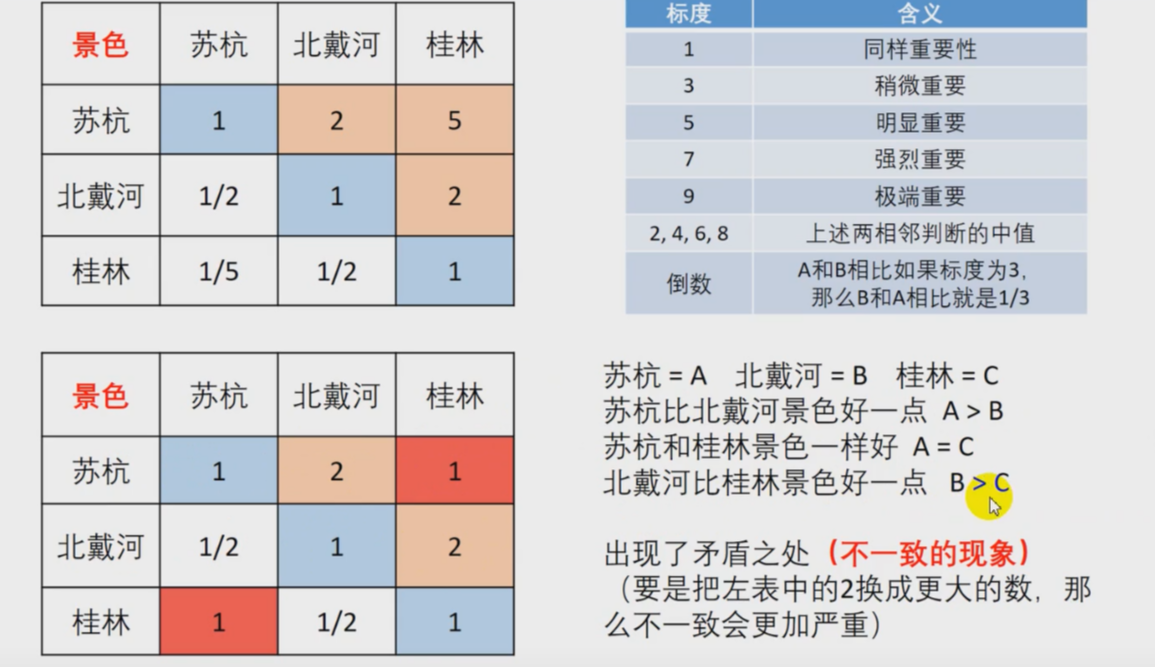
两个两个指标进行比较,最终根据两两比较的结果来推算出权重。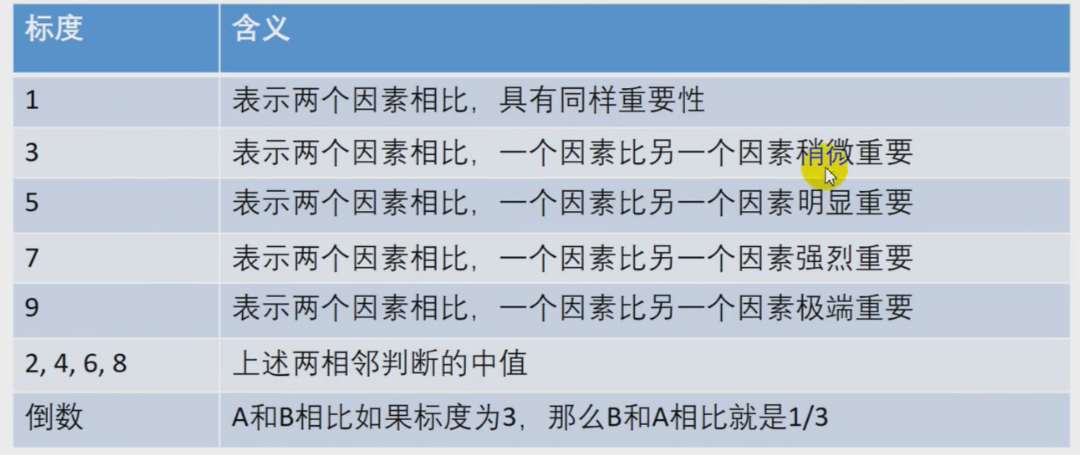

如何处理填写的数据

表可以转化成一个5x5的方阵 记该方阵为A 对应元素为$a_{ij}$

1. $$a_{ij}表示的意义是,与指标j相比,i的重要程度$$
2. $$当i=j时,两个指标相同,因此同等重要记为1,这就解释了主对角线元素为1$$
3. $$a_{ij}>0且满足a_{ij} \times a_{ji}=1 (我们称满足这一条件的矩阵为正互反矩阵)$$ 该矩阵就是层次分析法的判断矩阵

一致矩阵

判断矩阵可能存在Bug

若正互反矩阵满足

$$a_{ij} \times a{jk} = a_{ik}$$

则该矩阵为一致矩阵

注意:在使用判断矩阵求权重之前,必须对其进行一致性检验

$$\begin{bmatrix} a_{11} &a_{12} &\cdots &a_{1n} \\ a_{21} &a_{22} &\cdots &a_{2n} \\ \vdots &\vdots &\ddots &\vdots \\ a_{n1} &a_{n2} &\cdots &a_{nn} \\ \end{bmatrix}$$

为一致矩阵的充要条件是

$$\left\{ \begin{array} \leftline a_{ij} > 0\\ a_{11}=a_{22}=\cdots=a_{nn}\\ \begin{bmatrix} a_{i1},&a_{i2},&\cdots,&a_{in} \end{bmatrix}=k \begin{bmatrix} a_{11},&a_{12},&\cdots,&a_{1n} \end{bmatrix} \end{array} \right .$$

---

引理:A为n阶方阵,且r(A)=1,则A有一个特征值为tr(A),其余特征值均为0
因为一致矩阵的各行成比例,所以一致矩阵的秩一定为1
由引理可知:一致矩阵有一个特征值为m,其余特征值均为0
容易得到,特征值为n时,对应的特征向量刚好为

$$k \begin{bmatrix} \cfrac{1}{a_{11}},&\cfrac{1}{a_{12}},&\cdots,&\cfrac{1}{a_{1n}} \end{bmatrix}$$

---

引理:m阶正互反矩阵A为一致矩阵时当且仅当最大特征值入m=n
且当正互反矩阵A非一致时,一定满足入m>n

一致性检验

1. 计算一致性指标CI $$CI=\cfrac{\lambda_{max}-n}{n-1}$$
2. 查找对应的平均一致性指标RI
3. 计算一致性比例CR $$CR=\frac{CI}{CR}$$

如果CR<0.1,则可认为判断矩阵的一致性可以接受;否则需要对判断矩阵进行修正

计算权重

一致矩阵

取出其中一列数据计算即可,则每一位的权重

$$w_i=\frac{a_{i1}}{\sum\limits_{j=1}^na_{j1}}$$

非一致判断矩阵矩阵

1. 算术平均法求权重

1. 将判断矩阵按列归一化，即每个元素除以其所在列的和
2. 将归一化的各列相加（按行求和）
3. 将相加后向量中每个元素除以n即可得到权重向量 $$w_i=\cfrac{1}{n}\sum\limits_{j=1}^{n}{\cfrac{a_{ij}}{\sum\limits_{k=1}^{n}a_{kj}}}, (i=1,2,\cdots,n)$$

   2. 几何平均法

4. 将判断矩阵的元素按照行相乘得到一个新的列向量
5. 将新的向量的每个分量开n次方
6. 对该列向量进行归一化即可得到权重向量 $$w_i=\cfrac{(\prod\limits_{j=1}^{n}a_{ij})^{\frac{1}{n}}}{\sum\limits_{k=1}^{n}{(\prod\limits_{j=1}^{n}a_{kj})^{\frac{1}{n}}}}$$

   3.特征值法

7. 求出矩阵A的最大特征值以及其对应的特征向量
8. 对求出的特征向量进行归一化即可得到我们的权重

如何修正判断矩阵

如果$CR>0.1$,需要判断矩阵进行修正
向一致矩阵调整 使各列尽量成比例

计算各层元素对目标的权重

计算各层元素对目标的权重,并进行排序

局限性

1. 评价的决策层不能太多,太多的话n会很大,判断矩阵和一致矩阵差异
2. 如果决策层中指标的数据是已知的,那么我们如何利用这些数据来使评价的更加准确呢?