实现一个log函数
首先 有换底公式 logab=lnb/lna
由此 求log(b,a)可以转化为求lnb/lna
1
2
3
| double mylog(double b,double a){
return ln(b) / ln(a);
}
|
接下来只需要编写ln函数
常用的方法是采用多项式展开(泰勒级数)
ln(1+x)展开后为
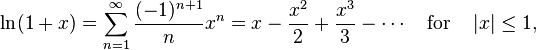
所以 先将ln(t)中 t 化为 2^k*(1+f) 的形式
其中sqrt(2)/2 < f < sqrt(2)
定义常量
1
2
3
4
| #define SQRT2 1.4142135623730950488016887242097
#define SQRT2D2 0.70710678118654752440084436210485
#define LN2H 6.93147180369123816490e-01
#define LN2L 1.90821492927058770002e-10
|
参数化约
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| int k=0;
if(x>SQRT2){
do
{
x/=2;
k++;
} while (x>SQRT2);
}else if(x<SQRT2D2){
do
{
x*=2;
k--;
} while (x<SQRT2D2);
}
|
此时 不难看出 ln(t)=ln(2^k*(1+f))=kln2+ln(1+f)
ln(2)在上方已经预先求出并定义
此时只需求出ln(1+f)
为了保证泰勒展开计算的精确度,要使f尽可能接近1,做如下变换
s=f/(2+f)
则ln(1+f)=ln(1+s)-ln(1-s)
此时 做泰勒展开 可得
ln(1+f)=ln(1+s)-ln(1-s)
=2(s-s^3/3+s^5/5+…)
做循环求出该多项式即可
求多项式
1
2
3
4
5
6
7
| for(int i=1;i<14;i+=2){
double s=x;
for(int c=1;c<i;c++){
s*=x;
}
res+=2*s/i;
}
|
测试用代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
| #include <stdio.h>
#include <math.h>
#define SQRT2 1.4142135623730950488016887242097
#define SQRT2D2 0.70710678118654752440084436210485
#define LN2H 6.93147180369123816490e-01
#define LN2L 1.90821492927058770002e-10
double ln(double x){
int k=0;
if(x>SQRT2){
do
{
x/=2;
k++;
} while (x>SQRT2);
}else if(x<SQRT2D2){
do
{
x*=2;
k--;
} while (x<SQRT2D2);
}
double res=k*LN2H+k*LN2L;
x-=1;
x=x/(2+x);
for(int i=1;i<14;i+=2){
double s=x;
for(int c=1;c<i;c++){
s*=x;
}
res+=2*s/i;
}
return res;
}
double mylog(double b,double a){
return ln(b)/ln(a);
}
int main(){
printf("%lf %lf",mylog(15,2),log(15)/log(2));
return 0;
}
|
测试结果
 下载源代码文件(log.c)
下载源代码文件(log.c)
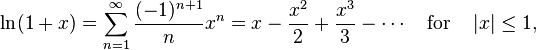
 下载源代码文件(log.c)
下载源代码文件(log.c)